Resume Integral dan Penerapannya dalam kehidupan sehari-hari

Resume Pertemuan Tanggal 17/09/2020
Kalkulus 2-D Oleh :

Nama : Husni Hadi

NIM  : 201931176

     Integral merupakan bentuk operasi matematika yang menjadi kebalikan (invers) dari operasi turunan dan limit dari jumlah atau suatu luas daerah tertentu. Berdasarkan pengertian tersebut ada dua hal yang dilakukan dalam integral sehingga dikategorikan menjadi 2 jenis integral. Pertama, integral sebagai invers/ kebalikan dari turunan disebut sebagai Integral Tak Tentu. Kedua, integral sebagai limit dari jumlah atau suatu luas daerah tertentu disebut integral tentu.

Integral Tak Tentu

    Integral tak tentu seperti sebelumnya dijelaskan merupakan invers/kebalikan dari turunan. Turunan dari suatu fungsi, jika diintegralkan akan menghasilkan fungsi itu sendiri. Perhatikanlah contoh turunan-turunan dalam fungsi aljabar berikut ini:

  • Turunan dari fungsi aljabar y = x3 adalah yI = 3x2
  • Turunan dari fungsi aljabar y = x3 + 8 adalah yI = 3x2
  • Turunan dari fungsi aljabar y = x3 + 17 adalah yI = 3x2
  • Turunan dari fungsi aljabar y = x3 – 6 adalah yI = 3x2

    Seperti yang sudah dipelajari dalam materi turunan, variabel dalam suatu fungsi mengalami penurunan pangkat. Berdasarkan contoh tersebut, diketahui bahwa ada banyak fungsi yang memiliki hasil turunan yang sama yaitu yI = 3x2. Fungsi dari variabel x3 ataupun fungsi dari variabel x3 yang ditambah atau dikurang suatu bilangan (misal contoh: +8, +17, atau -6) memiliki turunan yang sama. Jika turunan tersebut dintegralkan, seharusnya adalah menjadi fungsi-fungsi awal sebelum diturunkan. Namun, dalam kasus tidak diketahui fungsi awal dari suatu turunan, maka hasil integral dari turunan tersebut dapat ditulis:

f(x) = y = x3 + C

    Dengan nilai C bisa berapapun. Notasi C ini disebut sebagai konstanta integral. Integral tak tentu dari suatu fungsi dinotasikan sebagai:

\int f(x) dx

    Pada notasi tersebut dapat dibaca integral terhadap x”. notasi  disebut integran. Secara umum integral dari fungsi f(x) adalah penjumlahan F(x) dengan C atau:

\int f(x) dx = F(x)

    Karena integral dan turunan berkaitan, maka rumus integral dapat diperoleh dari rumusan penurunan. Jika turunan:

\frac{d}{dx}\frac{a}{(n+1)}x^{(n+1)} = ax^n

Maka rumus integral aljabar diperoleh:

\int ax^n dx = \frac{a}{(n+1)}x^{n+1} + C

dengan syarat n \neq 1.

Sebagai contoh lihatlah integral aljabar fungsi-fungsi berikut:

  • \int 4x^3dx=\frac{4}{(3+1)}x^{(3+1)}+ C = x^4 + C
  • \int \frac{1}{x^3}dx = \int x^{-3} dx = \frac{1}{(-3+1)}x^{-3+1}+C
    = -\frac{1}{2}x^{-2}+C = -\frac{1}{2x^2}+C
  • \int 4x^3 - 3x^2 dx = \frac{4}{(3+1)} x^{(3+1)} + \frac{3}{(2+1)}x^{(2+1)}+C
    = x^4+x^3+C
https://www.studiobelajar.com/integral/

Contoh Soal Integral :

1.Tentukanlah integral x jika diketahui g’(x) =  3x5+3

Untuk mengerjakan soal ini, kita dapat menggunakan sifat seperti soal pertama. Dalam soal ini, g’(x) merupakan turunan dari suatu fungsi. Berikut ini cara penyelesaiannya

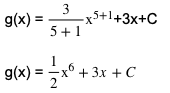
Nilai integral dari g’(x) adalah g(x) =  (1/2)x6 + 3x + C


https://rumuspintar.com/integral/contoh-soal/




Penerapan Integral dalam kehidupan sehari-hari :

1. Bidang Matematika  

a. Menentukan luas suatu bidang,
b. Menentukan volume benda putar,
c. Menentukan panjang busur

2. Bidang Ekonomi  

a. Mencari fungsi asal dari fungsi marginalnya (fungsi turunannya)
b. Mencari fungsi biaya total
c. Mencari fungsi penerimaan total dari fungsi penerimaan marginal
d. Mencari fungsi konsumsi dari fungsi konsumsi marginal,
e. Mencari fungsi tabungan dari fungsi tabungan marginal
f. Mencari fungsi kapital dari fungsi investasi

3. Bidang Teknologi  

a. Penggunaan laju tetesan minyak dari tangki untuk menentukan jumlah kebocoran selama selang waktu tertentu
b. Penggunaan kecepatan pesawat ulang alik Endeavour untuk menentukan ketinggian maksimum yang dicapai pada waktu tertentu
c. Memecahkan persoaalan yang berkaitan dengan volume, panjang kurva, perkiraan populasi, keluaran kardiak, gaya pada bendungan, usaha, surplus konsumen

4. Bidang Fisika  

a. Untuk analisis rangkaian listrik arus AC
b. Untuk analisis medan magnet pada kumparan
c. Untuk analisis gaya-gaya pada struktur pelengkung

5. Bidang Teknik

    Penggunaan Integral dapat membantu programmer dalam pembuatan aplikasi dari mesin-mesin yang handal. Misal: Para enginer dalam membuat desain mesin pesawat terbang.

6. Bidang Medis  

    Dosimetri adalah ri radioterapi, intinya dosimetri tersebut memakai high energy ionizing radiation, salah satu contohnya yaitu sinar-X. Disini ilmu matematika khususnya integral sangat berpengaruh dalam proses pengerjaanya, dimana penembakan laser nantinya membutuhkan koordinat yang tepat. Pada integral dibahas volume benda putar dengan metode cakram, cincin, dan lain lain (dengan begini dapat mengukur volume tumor, jikalau pasca penembakan laser volume menurun, maka operasi berhasil).


    Nah! bagaimana? banyak kan manfaat dari integral? dan sekarang kita sudah tau, jadi jangan anggap pelajaran itu tidak ada manfaatnya, ini baru contoh kecil loh teman-teman, jadi jangan sampai disini aja ya menggali pengetahuannya, mari gali lebih banyak lagi ilmu agar kita tahu manfaat dan bisa menerapkan nya dalam kehidupan kita.

    Sampai disini ya teman-teman kalau ada kesalahan saya minta maaf ya bisa di komentar dibawah kalau saya ada salah biar bisa saya koreksi. Komentar dari teman-teman bisa membantu saya, jangan lupa di bagikan ya jika ini sangat bermanfaat, agar ilmunya dapat berkembang dan bisa bermanfaat bagi orang banyak, Terima kasih.

Komentar

Posting Komentar